What if I told you that your brain – the same incredible organ that can recognize faces 👤, compose symphonies 🎵, and contemplate the universe 🌌 – is actually quite terrible at solving simple problems? 🤯
Today, we’re going to explore the fascinating world of cognitive biases through 10 deceptively simple puzzles. Each one is designed to make your brain stumble 🧠💥, not because you’re not smart enough, but because of how human thinking actually works.
You see, psychologist Daniel Kahneman identified two systems of thinking: System 1 ⚡ is fast, intuitive, and automatic – it wants quick answers with minimal effort. System 2 🐌 is slow, deliberate, and analytical – it checks the receipts, but requires more mental energy. Many of these puzzles trick us into using System 1 when we really need System 2.
Ready to see how your brain handles these challenges? 🎯 Keep track of your score, and don’t worry if you get some wrong – you’re in good company. I still don’t understand problem #10, even though I know the “correct” answer. 🤷♂️
Let’s begin… 🚀
🕒 Problem 1: The Clock Hands

Question: It’s 3:00 on this analog clock. ⏰ Approximately how long do we have to wait until both hands line up with each other perfectly? 🤝
Answer: About 16 minutes and 22 seconds. ⏱️
Explanation:
Did you guess 9 minutes? 🤔 Or maybe you thought they’d align at 3:15? That’s your System 1 thinking at work! ⚡
The hour hand moves continuously, not in discrete jumps. At 3:00, the minute hand needs to “catch up” to where the hour hand will be when they align. Since the hour hand moves 0.5 degrees per minute and the minute hand moves 6 degrees per minute, the relative speed is 5.5 degrees per minute. 📐
At 3:00, they’re 90 degrees apart, so: 90 ÷ 5.5 = approximately 16.36 minutes. 🧮
This demonstrates pattern-seeking bias 🔍 – we expect alignment to happen at “obvious” times like 3:15, when the math reveals something more precise and counterintuitive. 🎯
📚 Problem 2: The Never-Ending Book

Question: A book has 100 pages. 📖 You read half the remaining pages each day. How many days does it take to finish the book? 🤷♀️
Answer: You never finish the book. ♾️
Explanation:
Day 1: Read 50 pages (50 remaining) 📄
Day 2: Read 25 pages (25 remaining) 📄
Day 3: Read 12.5 pages (12.5 remaining) 📄
Day 4: Read 6.25 pages (6.25 remaining) 📄
…and so on forever. 🔄
Since you’re always reading half of what remains, there will always be something left – you approach zero but never reach it. 📉 This is an example of finite thinking bias 🧠, where our System 1 assumes completion must be possible in a reasonable timeframe.
Mathematically, this is a geometric series that converges to 100 but never actually reaches it. 🔢
🪙 Problem 3: The Double Coin Flip

Question: You flip two coins 🪙🪙, knowing that at least one of them will definitely land on heads. What is the probability of flipping double heads? 🎯
Answer: 1 in 3 (or 33.33%) 📊
Explanation:
If you said 1 in 2, you fell for conditional probability bias! 🪤 Here’s why:
All possible outcomes when flipping two coins: 🪙
– Heads, Heads (HH) ✅
– Heads, Tails (HT) ✅
– Tails, Heads (TH) ✅
– Tails, Tails (TT) ❌
Since we know at least one is heads, we eliminate TT. That leaves us with three equally likely outcomes: HH, HT, and TH. 🎲
Only one of these three outcomes is double heads, so the probability is 1/3. 📈
System 1 thinking simplifies this to “one coin is heads, so the other is 50/50,” but that ignores the conditional information we were given. ⚡🧠
🔥 Problem 4: The Two Ropes

Question: You have two ropes. 🪢🪢 Each rope takes exactly 60 seconds to burn completely when lit at one end. The ropes burn at inconsistent rates. How do you measure exactly 30 seconds using these ropes? ⏰
Answer: Light both ends of one rope simultaneously. 🔥🔥
Explanation:
When you light both ends of a rope that takes 60 seconds to burn from one end, it will burn completely in exactly 30 seconds – the flames meet in the middle! 💥
Most people overthink this, assuming they need to use both ropes or cut them somehow. ✂️ This demonstrates functional fixedness 🔒 – we get stuck thinking about ropes being lit “normally” (from one end) because that’s how the problem described them initially.
The elegant solution requires breaking free from conventional thinking and realizing that lighting both ends simultaneously halves the burn time, regardless of the rope’s inconsistent burn rate. 🧠💡
⚾ Problem 5: The Bat and Ball

Question: A bat and ball cost $1.10 total. 💰 The bat costs $1.00 more than the ball. How much does the ball cost? ⚾
Answer: The ball costs 5 cents. 🪙
Explanation:
If you said 10 cents, you’re not alone – but you’re wrong! ❌ Let’s check:
– If ball = 10¢ and bat = $1.10, then bat costs only $1.00 more than ball ❌
– If ball = 5¢ and bat = $1.05, then bat costs exactly $1.00 more than ball ✅
This classic puzzle demonstrates several biases: 🧠
– Anchoring bias ⚓: The $1.00 difference sticks in our mind
– Confirmation bias ✅: 10 cents “feels” reasonable, so we don’t double-check
– System 1 thinking ⚡: We grab the first plausible answer without verification
The correct equation is: Ball + (Ball + $1.00) = $1.10 🧮
Solving: 2×Ball = $0.10, so Ball = $0.05 📊
🌸 Problem 6: The Lily Pad
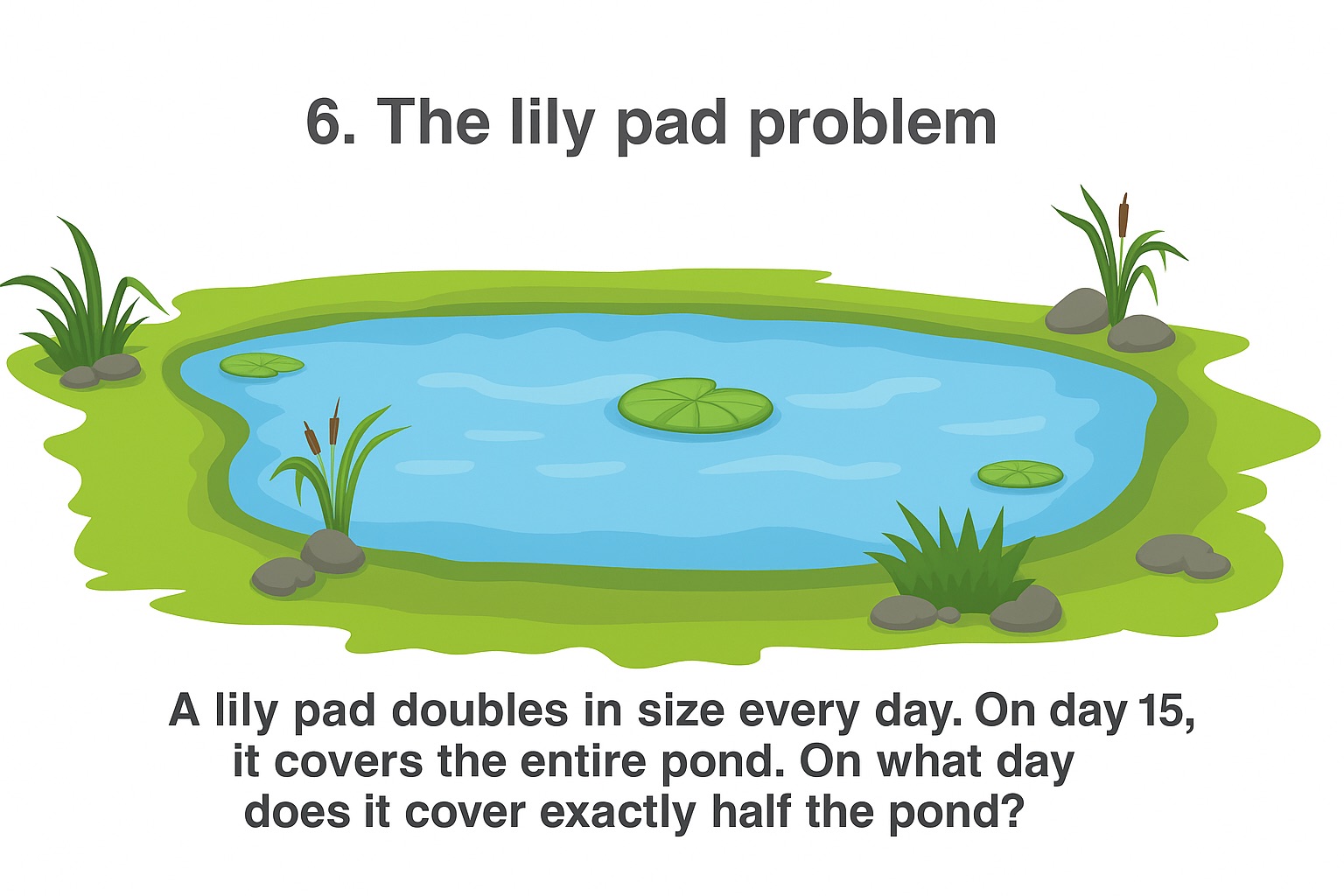
Question: A lily pad doubles in size every day. 🌱➡️🌿➡️🌸 On day 15, it covers the entire pond. On what day does it cover exactly half the pond? 🏊♀️
Answer: Day 14 📅
Explanation:
If the lily pad covers the entire pond on day 15, and it doubles every day, then it must have covered half the pond the day before – day 14! 🤯
Many people guess day 7 or 8, falling victim to linear thinking bias 📏. We intuitively want to divide 15 by 2, but exponential growth doesn’t work that way. 📈
This also shows anchoring bias ⚓ – we fixate on the number 15 and try to manipulate it arithmetically, when the solution requires understanding the doubling pattern. 🔄
Exponential growth is counterintuitive to our brains 🧠, which evolved to think in linear terms about most everyday phenomena. 🦕
🐸 Problem 7: The Frog in the Well
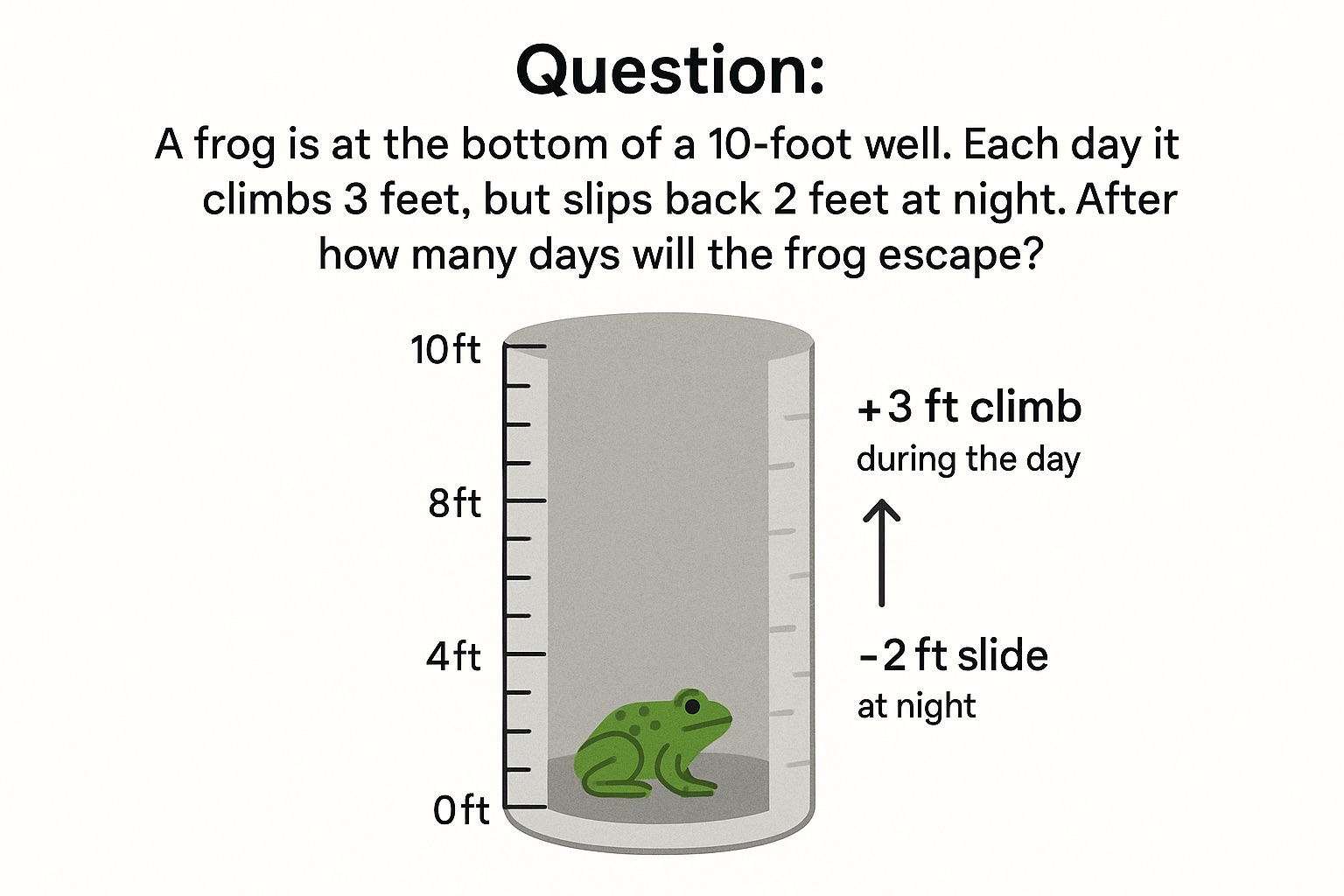
Question: A frog is at the bottom of a 10-foot well. 🕳️ Each day it climbs 3 feet 📈, but slips back 2 feet at night 📉. After how many days will the frog escape? 🐸
Answer: 8 days 📅
Explanation:
Let’s track the frog’s progress: 🐸
– Day 1: Climbs to 3ft, slips to 1ft 📍
– Day 2: Climbs to 4ft, slips to 2ft 📍
– Day 3: Climbs to 5ft, slips to 3ft 📍
– Day 4: Climbs to 6ft, slips to 4ft 📍
– Day 5: Climbs to 7ft, slips to 5ft 📍
– Day 6: Climbs to 8ft, slips to 6ft 📍
– Day 7: Climbs to 9ft, slips to 7ft 📍
– Day 8: Climbs to 10ft and ESCAPES! 🎉 (No slipping back)
Many people calculate the net gain (1 foot per day) and conclude 10 days, but this ignores the escape condition. 🚪 Once the frog reaches the top on day 8, it doesn’t slip back down.
This demonstrates how System 1 thinking ⚡ averages out the pattern without considering the boundary conditions that require more careful System 2 analysis 🐌.
🧦 Problem 8: The Sock Drawer
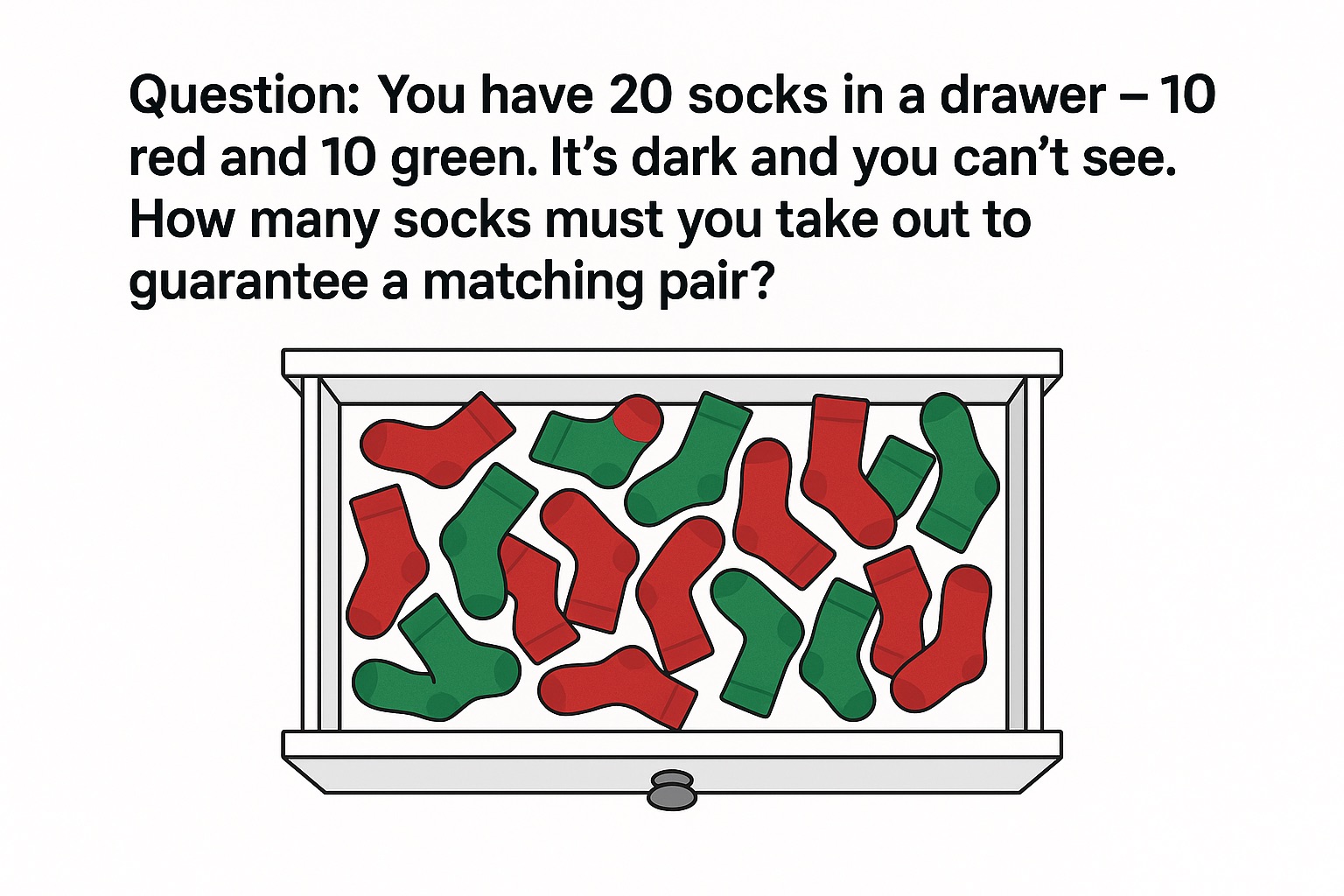
Question: You have 20 socks in a drawer – 10 red ❤️ and 10 green 💚. It’s dark 🌙 and you can’t see. How many socks do you need to grab to guarantee a matching pair? 👥
Answer: 3 socks 🧦🧦🧦
Explanation:
Think about the worst-case scenario: 😱
– First sock: Could be red ❤️ or green 💚
– Second sock: Could be the other color 🔄
– Third sock: MUST match one of the first two! ✅
With only two colors available, grabbing three socks guarantees at least two of the same color. 🎯
Many people think you need many more socks, falling for abundance bias 📚 – assuming “more is safer.” System 1 thinking suggests that 11 socks feels right because it’s “over half,” but this completely misunderstands the problem. 🤔
This is an application of the Pigeonhole Principle 🕳️: if you have more items than containers, at least one container must contain multiple items. 📦
⚙️ Problem 9: The Widget Machine
Question: 5 machines make 5 widgets in 5 minutes. 🏭 How long would it take 100 machines to make 100 widgets? ⏰
Answer: 5 minutes ⏰
Explanation:
Let’s break this down: 🧮
– 5 machines make 5 widgets in 5 minutes ⚙️
– Therefore: 1 machine makes 1 widget in 5 minutes 🎯
– So: 100 machines make 100 widgets in… 5 minutes! 🤯
Many people answer 100 minutes, falling for the proportionality heuristic 📊. The symmetry of “5-5-5” tricks us into thinking everything scales proportionally, including time. ⚖️
But machines work in parallel! 🔄 If each machine independently makes one widget in 5 minutes, then 100 machines working simultaneously will produce 100 widgets in the same 5 minutes. ⚡
This demonstrates how pattern recognition 🧩 can mislead us when we overgeneralize mathematical relationships. 📈
🚗 Problem 10: The Monty Hall Problem
Question: You’re on a game show with three doors. 🚪🚪🚪 Behind one is a car 🚗, behind the other two are goats 🐐🐐. You pick Door 1. The host (who knows what’s behind each door) opens Door 3, revealing a goat 🐐. Should you stick with Door 1 or switch to Door 2? 🤔
Answer: You should switch to Door 2. 🔄
Explanation:
[Author’s note: Like the original presenter, I find this counterintuitive, but here’s the mathematical explanation] 🤷♂️
When you initially chose Door 1, you had a 1/3 chance of being right and a 2/3 chance of being wrong. 📊
The key insight: The host’s action gives you information. 📡 The host knows where the car is and will always reveal a goat. When the host opens Door 3, they’re not making a random choice – they’re strategically eliminating one of the losing options. 🎯
Here’s why switching gives you 2/3 probability: 🧮
– Initially: P(car behind Door 1) = 1/3, P(car behind Doors 2 or 3) = 2/3 📈
– After host reveals goat behind Door 3: P(car behind Door 1) = still 1/3 📍
– But now all of that 2/3 probability that was split between Doors 2 and 3 gets concentrated on Door 2 alone 🎯
Think of it this way: You’re essentially choosing between your original door (1/3 chance) and both of the other doors combined, with the host helping you by eliminating the goat from that pair. 🤝
This violates our intuition about probability and demonstrates how additional information can change the mathematical landscape in unexpected ways. 🌍🤯
🎬 And as always… thanks for thinking.
How did you do? 📊 Did your brain fall for these cognitive traps? 🪤 Don’t feel bad if you did – these puzzles reveal universal features of human psychology, not personal shortcomings. 🧠💭
The fascinating thing is that even when we know about these biases, we often still fall for them. 🔄 Our System 1 thinking is so fast and automatic that it’s hard to override, even with knowledge of its limitations. ⚡
But awareness is the first step. 👀 By understanding how our minds can be tricked, we become better at recognizing when to slow down and engage our more analytical System 2 thinking. 🐌🧠
In a world full of complex decisions, quick judgments, and information overload 📱💻, these skills are more valuable than ever. Because the most important puzzles aren’t the ones in quiz videos – they’re the ones we encounter every day in real life. 🌍
And that’s something worth thinking about… or is it? 🤔
More from Fun
You Won’t Believe What People Are Googling: Auto-Suggest Nightmares
Without a doubt, Google autocomplete is one of the most illuminating windows into the human psyche. It’s not some cold, …
Seeing Faces in Everyday Objects? Here’s What’s Really Happening
Human cognition is both a marvel and a mystery. It is a tool forged in the fires of evolution, honed …
Can You Tell If This Art Is Human or AI? Most People Can’t!
Once upon a time, art was the way humans flexed, a way to show off our emotions, imagination, and skill. …